Thoughts About A Science Of Evidence
 0%
0%
 Author: DAVID A. SCHUM
Author: DAVID A. SCHUM
Publisher: www.ucl.ac.uk
Category: Western Philosophy

Author: DAVID A. SCHUM
Publisher: www.ucl.ac.uk
Category: visits: 9436
Download: 4131
Comments:
- THOUGHTS ABOUT A SCIENCE OF EVIDENCE
- 1.0 A STANDPOINT IN THIS ACCOUNT OF A SCIENCE OF EVIDENCE
- 2.0 SOME BEGINNINGS
- 3.0 CONCEPTS OF EVIDENCE AND SCIENCE: THEIR EMERGENCE AND MUTATION
- 3.1 On the Concept of Evidence.
- 3.2 On the Concept of Science and Its Methods
- 4.0 ELEMENTS OF A SCIENCE OF EVIDENCE
- 4.1 Classification of Evidence
- 4.2 Studies of the Properties of Evidence.
- 4.2.1 On the Relevance of Evidence
- 4.2.2 On the Credibility of Evidence and Its Sources.
- Credibility Attributes: Tangible Evidence
- Competence and Credibility Attributes: Testimonial Evidence
- Credibility Attributes.
- 4.2.3 The Inferential Force, Weight or Strength of Evidence
- Bayes' Rule and the Force of Evidence
- Evidential Support and Evidential Weight: Nonadditive Beliefs
- Evidential Completeness and the Weight of Evidence in Baconian Probability
- Verbal Assessments of the Force of Evidence: Fuzzy Probabilities
- 4.3 On the Uses of Evidence
- 4.3.1 On the Inferential Roles of Evidence
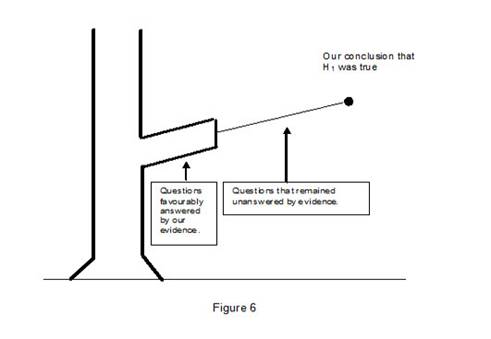
- Supporting Hypothesis H.
- Negating Hypothesis H
- 4.3.2 Stories from Evidence and Numbers
- 4.4. Discovery in the Science of Evidence
- 4.4.1 Discoveries about Evidence
- 4.4.2 Evidence Science and the Discovery of New Evidence
- Generating Evidence from Argument Construction
- Evidence Marshaling and Discovery
- Mathematics and the Discovery of Evidence
- 4.5 A Stronger Definition of a Science of Evidence
- 5.0 AN INTEGRATED SCIENCE OF EVIDENCE
- 5.1. The Science of Evidence: A Multidisciplinary Venture
- 5.2 The Science of Complexity: A Model
- 5.3 A Science of Evidence: Who Should Care?
- 6.0 IN CONCLUSION
- NOTES