Alhassanain(p) Network for Heritage and Islamic Thought

4.3.1 On the Inferential Roles of Evidence

I focus now on Twining's comment given above and his phrase: …"information has a potential role as relevant evidence if it tends to support or tends to negate, directly or indirectly, a hypothesis or probandum". Wigmore has given us a very useful classification of the roles evidence can play in the context of proof[153]. In discussing these evidential roles, Wigmore used terms that are encountered in adversarial processes in our system of laws. But I can make them quite general in their application to inferences in any context. I recall here Stephen Toulmin's comment on adversarial processes and the case we try to make from evidence in any context, and his saying that "logic is generalized jurisprudence"[154].

To make the following comments as general as I can I am going to assume just one person making an inference, namely you.  We don't care about the context or substance of this inference. You are trying to reach a conclusion concerning whether hypothesis H is true or not. We might suppose that you have proposed hypothesis H. The only thing we will assume is that you are open-minded and are willing to consider evidence bearing upon both of the hypotheses: H and not-H. The evidence you will encounter may be tangible or testimonial in form and you may receive it as a result of your own efforts as well as the efforts of others from whom you may request information. You will note in this example that several of the forms, mentioned in Figure 1, and combinations of evidence that I said were "substance-blind" will arise in this example. This will satisfy Poincaré's emphasis on the importance of classification in science.

Supporting Hypothesis H.

First suppose you believe that if event E occurred, it would be directly relevant but not conclusive evidence favouring H. You then find evidence E*, that this event E occurred. This evidence may be a testimonial assertion or an item of tangible evidence. In Wigmore's analysis this would be called aproponent's assertion , if we regarded you as the "proponent" of hypothesis H. You are concerned of course about the credibility of the source of E*. Suppose you obtain ancillary evidence favourable to the credibility of this source. This would enhance your belief that event E did occur. Suppose, in addition, you query another source who/that corroborates what the first source has said; this second source also provides evidence that event E occurred. You then gather ancillary evidence that happens to favour the credibility of this second source. But you also gather evidence in support of the generalization that licenses the relevance linkage between event E and hypothesis H. This evidence would strengthen this linkage.

But you know about other events, if they occurred, would also support hypothesis H. In particular, you believe that event F would converge with event E in favouring H. You gather evidence F*, that event F occurred. You might gather ancillary evidence favourable to the credibility of the source of F, and you might also gather corroborative evidence from another source that event F occurred. You might, in addition, gather further ancillary evidence to strengthen the generalization that licenses your inference from event F to hypothesis H. So, now you have two lines of evidence which, together, would increase the support for hypothesis H. You may of course know of think of other events that would converge in favouring H.

Wigmore was no probabilist, that would have been asking too much of him, given all of his other accomplishments regarding evidence and proof. Study of probabilistic matters concerning the inferential force of evidence suggests additional ways in which we you can use evidence to support hypothesis H. First, suppose that evidence E* is testimonial and came from a source named Mary. You begin to think that the fact that Mary told you that event E occurred means more than it would if someone else had told you about E. In fact, what you know about Mary's credibility makes her testimony more valuable than if you knew for sure that event E occurred. In short, what we know about a source of evidence can often be at least as valuable as what the source tells us. I have captured this subtlety associated with testimonial evidence mathematically in a recent report[155].

Another subtlety, this time involving events E and F. can be captured that would often greatly increase the support that evidence of these events could provide for hypothesis H. Earlier in Section 4.1.2 I mentioned how items of convergent evidence, favouring the same hypothesis, can often be synergistic in their inferential force. You might believe that evidence of events E and F, taken together, would favour hypothesis H much more strongly than they would if you considered them separately or independently. This synergism can be captured in probabilistic terms[156].

These are all roles that evidence can play in support of some hypothesis. But we agreed that you are open-minded and will carefully consider counterevidence that would negate H or would favour not-H.

Negating Hypothesis H

A colleague appears who has never shown any great enthusiasm for a belief that hypothesis H is true. So far you have said that events E and F would favour H. But your colleague challenges the credibility of the sources of evidence about these events by first producing ancillary evidence that disfavours their credibility. In addition, your colleague might produce contradictory evidence from sources who/that will say that either or both of the events E and F did not occur. Wigmore referred to this evidence as constitutingopponent's denial that events E and F occurred.

But your colleague might instead, or in addition, have ancillary evidence that weakens the generalizations you have asserted that link events E and F to hypothesis H. Such evidence would tend toexplain away what you have said was the significance of events E and F. This ancillary evidence would allow your colleague to say: "So what if events E and F did occur, they have little if any bearing on hypothesis H". Wigmore termed this situationopponent's explanation .

Your colleague has yet another strategy for negating H. She might say the following: "So far you have only considered events [E and F] that you say would favour H. Are you only going to consider events you believe favour H? I have gathered evidence J* and K* about events J and K that I believe disfavours H. Wigmore termed this situationopponent's rival evidence . In this situation you would have to cope with what I termed divergent evidence. There is no contradiction here since J and K involve different events and might have occurred together with events E and F. Events J and K simply point in a different F.

inferential direction than do events E and F.

But your colleague has a final approach to undermining an inference that H is true; it involves what you might have said about the synergism involving events E and F. Your colleague says: "You have said that evidence about events E and F taken together have much more force than the would have if we considered the separately. In other words you are   saying that event F has more force in light of the occurrence of E than it would have if we did not consider E. But I argue that the occurrence of E would make F redundant to some degree and so I argue that they mean less when taken together than they would do when considered separately.

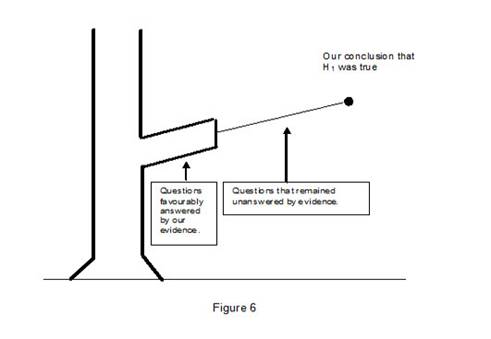
In providing this illustration of the various roles evidence plays, it was not actually necessary for me to suppose that you experienced a colleague who would use these evidential strategies for undermining a belief in H. If you were indeed open minded in your inferential approach, you would have played your own adversary by considering how evidence favourable to H could be attacked or countered in these various ways by other evidence. Your conclusion may well have been that not-H is true in spite of your initial belief that H was true. What this example illustrates is the necessity for us to be unbiased or objective in the gathering and evaluation of evidence in the inferences we make from evidence. We might say that we are well served when we play the role of our own "loyal opposition" in the inference tasks we face. This is true even if we often face the often "not so loyal opposition" from our critics.

4.3.2 Stories from Evidence and Numbers

I begin by acknowledging the many studies currently being undertaken in which masses of evidence and complex processes are being analyzed in probabilistic ways in a variety of important contexts including law, medicine and intelligence analysis. Consider Figure 2 again that shows two very simple illustrations of the different forms of inference networks that have been analysed probabilistically. I will use both the Wigmore analysis of a mass of evidence and a certain process model to illustrate how it is possible, and usually necessary, to construct alternative stories that might be told about the inferential force of a mass of evidence. My examples will involve the use of Bayes' rule, but similar analyses can be performed using Shafer's belief functions or Cohen's Baconian probabilities.

Both of the examples I will discuss involve what is termed "task decomposition" or "divide and conquer". In such decompositions, an obviously complex inference task is broken down into what are believed to be its basic elements. Wigmore's analytic and synthetic methods of analyzing a mass of evidence is a very good example. We first list all of the evidence and sources of doubt we believe appear in arguments from evidence to what we are trying to prove or disprove from it [a key list], and then construct a chart [or inference network] showing how we believe all of these pieces fit together. As I have mentioned, we can describe this process as one of trying to "connect the dots".

Suppose we have a mass of evidence in our analysis and an inference network based on this evidence that has survived a critical analysis designed to uncover any disconnects or non sequiturs in the arguments we have constructed. The next step is to assign probabilities that will indicate the strength with which the probanda, sources of doubt, or probabilistic variables are linked together. These probabilities come in the form of the likelihoods I described in Figure 5. All the arrows in the two diagrams in Figure 2 indicate these probabilistic linkages expressed in terms of likelihoods. Let us suppose that we all agree that the inference network we have constructed captures the complex arguments or elements of the process we are studying. But where do these linkage probabilities come from? In some very rare instances we might have a statistical basis for estimating these probabilities from relative frequencies. But in most instances many or most of these probabilities will rest on epistemic judgments we make. In the two examples I will provide,all of the probabilities rest on subjective judgments. Here is where the necessity for telling alternative stories arises.

Though we agree about the structure of our inference network we may find ourselves in substantial disagreement about the likelihoods linking elements of our argument together. Suppose we are interested in determining the overall force or weight of the evidence we are considering. How do our differences in these likelihood ingredients affect the force of the evidence we are considering? We might say that our different beliefs about these probabilistic ingredients allow us to tell different "stories" about the force of the evidence we are considering. The "actors" in our stories consist of the items of evidence we have. The "plots" of our stories are provided by the likelihoods we have assessed. When your likelihoods are different from mine we are essentially telling possibly different stories based on the same evidence, or involving the same actors. We are of course interested in the extent to which our stories end in telling us about the force of the evidence we have. How your story ends may be quite different from the ending of my story, but not necessarily. The metaphor of telling stories from evidence is certainly appropriate. It describes a process that is repeated every day involving the different stories told from the same evidence by opposing attorneys in trials at law. They use the same actors to tell different stories.

How do we tell how our different stories about the force of evidence will end? This is where mathematics comes to our assistance. It involves the process of what is termedsensitivity analysis . We have equations stemming from Bayes' rule that tell us how to combine your likelihoods and my likelihoods in calculations of the force of all the evidence we are considering.  In short, these equations supply endings to your story and my story about the aggregate force of the evidence. Here comes Carnap's comparison and numerical concepts again in a science of evidence. Our stories are told numerically but they can easily be translated into words. Then we can compare our stories to observe the extent to which our differing likelihood ingredients have affected determinations of the force of the evidence.

But there is an important characteristic of the equations we use to combine these  likelihood ingredients; they are allnon-linear . What this means is that these equations can produce many "surprises" that would never result from linear equations in which "the whole is always equal to the sum of its parts". What will happen is that, on some occasions, the fact that our assessed likelihoods are quite different makes little difference in the ending of our two stories; we are telling two stories that have the same or nearly the same ending. But on other occasions even exquisitely small differences in our likelihood ingredients will produce drastic differences in our stories about the force of our evidence.

Jay Kadane and I used the process of sensitivity analysis just described in our probabilistic analysis of parts of the evidence in the case of Sacco and Vanzetti. We used this process to tell different stories on behalf of the prosecution and of the defence in this case[157].  As I mentioned above, we used the same evidence in telling these stories on behalf of the parties involved in this trail. Here are two examples of the kinds of stories we told and how we told them.

The first involved what Wigmore termedconcomitant evidence, that involved what Sacco was doing at the time of the crime. Two of the witnesses I have already mentioned, Lewis Pelser and Lewis Wade. They were the prosecution's "star" witnesses. Recall that Pelser said he saw Sacco at the scene of the crime when it occurred, and Wade said he saw someone who looked like Sacco at the scene of the crime when it occurred. But there were five defence witnesses, four of whom were just across then street from where the payroll guard Berardeiil was shot. They all said the neither Sacco nor Vanzetti was at this scene when the shooting occurred. A fifth defence witness testified that Sacco was not at the scene about 15 minutes before the crime occurred.

The Wigmorean argument structure for the evidence just described is simple enough so that were able to write out the exact equations necessary for combining the likelihoods in this argument structure. Using these equations we told ten different stories, five on behalf of the prosecution and five on behalf the defence[158]. In the process of telling these ten stories we varied the value of likelihoods such as those that concern the credibility of the witnesses, and other matters such as those concerning the probability of someone looking like Sacco being at the scene, given that Sacco was not there. The ten stories we told all have different endings as far as the weight of this evidence favouring either the hypothesis that Sacco did shoot the payroll guard or the hypothesis that Sacco did not shoot the payroll guard. As I noted above, these stories often have surprising endings. For example, by varying Pelser's credibility by apparently just a small amount we can effectively destroy the contribution of his testimony to the weight of the combination of evidence being considered. Some of the stories we told illustrated how Bayes'  rule captures the possible redundance of Pelser's and Wade's testimonies.

We also considered much more complex aggregates of the evidence in this case[159]. One combination of evidence concerned Bullet III I mentioned earlier and the Colt automatic alleged to be the one Sacco had in his possession when he was arrested. The argument structure here is sufficiently complex that it prevents us from writing out equations for the force of evidence. The inference network we constructed for this ballistics evidence requires 42 assessments of likelihoods. But thanks to the truly outstanding works of several probabiliists, we now have computer-based systems that "know" what the necessary equations should be for any appropriate argument structure [a DAG] we can construct, whether it is a Wigmore evidence chart or a process model such as the ones I illustrated in Figure 2[160]. The stories we told on behalf of the prosecution and defence were designed to capture important conditional dependencies among probanda or propositions appearing on our inference network. For example, evidence that Bullet III was fired through Sacco's Colt points toward Sacco's guilt, but not very strongly. Someone else may have fired this weapon during the crime. But this evidence means more when we take into account other evidence that Sacco fired a weapon at the scene of the crime when it  was committed. The credibility of all of this evidence is so important.

We were pleased to note that the stories we told from numbers in the Sacco and Vanzetti case were included in a work by John Allen Paulos, a mathematician whose books enjoy a very wide following. In a recent book on what he terms the hidden mathematical logic behind stories[161], he describes the usefulness of the stories we told from numbers in the Sacco and Vanzetti case and argues that the Wigmorean analysis underlying these stories would have been useful in other complex cases such as the trial of O. J. Simpson.

I make one final point about telling stories from numbers based on inference networks constructed from evidence. I have said nothing so far about the role ofexperiments in a science of evidence. The process of sensitivity analysis is a form of experimentation in which we vary the probabilistic ingredients of equations based on a given inference network. We do so in order to see how the equations will behave [i.e what different stories they will tell] in response to these changes in their ingredients. But do all of the stories told based on an inference network make sense?  Sensitivity analysis is also a process for testing the inference network itself. As I have mentioned, inference networks we construct are products of our imaginative and critical reasoning. How do we test to see if the network we have constructed makes sense in allowing us to draw conclusions of interest to us? Sensitivity analysis allows one kind of test: Does our network allow us to tell stories that make sense when we vary the ingredients of these stories in more or less systematic ways? This form of experimentation is one I have used for years in testing the inferential consequences of arguments I have constructed from a wide variety of forms and combinations of evidence[162]. A science of evidence does allow experimental tests of our views about how we believe evidence to be related to matters we are trying to prove or disprove.

4.4. Discovery in the Science of Evidence

The third OED definition of science, that I mentioned in my opening remarks in Section 4.0, is restrictive in the sense that it makes necessary for a science to have "reliable methods for the discovery of new truths in its own domain". I have two responses here, the first concerns how we extend our knowledgeabout evidence and its properties and uses; this involves how we learn more about evidence itself. The second concerns how a science of evidence can provide methods for enhancing discovery-related activities in any discipline or context in which this science may be applied. So in this sense we have both basic and  applied interests to consider as far as concerns discovery in the science of evidence.

4.4.1 Discoveries about Evidence

In Section 3.0 I considered how the concepts ofevidence and ofscience have emerged and changed over the ages. At no point did I argue that these two concepts are now fixed for all time. Thus, a science of evidence is in the process of emergence in which we hope to learn more about evidence as we continue to study it. For example, I have offered a categorization of recurrent forms and combinations of evidence that I advertised as being "substance-blind" only in the sense that it tells us what kinds of evidence we have. But I never advertised that my classification could not be improved or that other useful classifications could never be made. You might, for example, think of a type of evidence that I have left out of the rows in Figure 1. If so, please tell me about it.

What we wish to avoid are problems the philosopher Imre Lakatos identified in connection with what he calledresearch programs [163]. He called research programsprogressive to the extent that they continue to have heuristic power in generating new facts about the phenomena of interest. If they fail to do this, and just continue to account for already observed facts, Lakatos called themregressive research programs. Given the richness of the contexts in which evidence is used and studied, we run little risk of a science of evidence becoming regressive any time soon, provided that we share our experiences and thoughts about evidence with each other. Phil Dawid's emphasis in his proposal to the Leverhulme Foundation emphasized anintegrated science of evidence. I have always interpreted an integrated science of evidence to involve the necessity of identifying and exploiting our varied experiences and thoughts about evidence. I will give just two examples of how such sharing has benefited me in my work on evidence. I return to the integrated nature of a science of evidence in Section 5.0.

I have always marvelled that there are so many important evidential and inferential subtleties or complexities that often lie just below the surface of even the "simplest" of evidence-based reasoning tasks [if there are any such things as "simple" inferential tasks]. I spent many years of my work on evidence trying to identify and understand these subtleties so that they could be exploited in the conclusions we must draw from evidence. These subtleties involve any or all of the evidence credentials I have mentioned: relevance, credibility and inferential force or weight. Many years ago I recognised that nearly every law case I read revealed some new subtlety I should examine. Many of those I have studied were first revealed to me in law cases, some that took place centuries ago.

But I have often observed subtleties revealed in the works of others interested in the study of various kinds of evidence. As an example, I now refer to the work of C. A. J. Coady, a philosopher interested in the study of testimony[164]. As expected, Coady carefully examines the epistemological foundations for testimonial evidence. But one chapter of his work was especially interesting to me, his Chapter 10  entitled;Astonishing Reports . This chapter concerns testimonial evidence of events either contrary to the laws of nature, or testimony about unusual events that would conform to these laws. The study of testimony about miracles has occupied the attention of probabilists and others for centuries[165]. And it is still a still a topic of research today[166]. I hope to give further study to these topics in future. In my probabilistic studies there are very interesting terms appearling that concern the rareness or improbability of the events reported in testimony. Since the 1600s it has been expected that the rareness of the event reported, in addition to the credibility of the source reporting the event, are factors that determine the force of testimonial evidence about this event. But the relationship between these ingredients was never made clear in any studies I could find. I am just vain enough to conclude that my analysis of this rareness-credibility problem makes the nature of this relationship clear. It turns out that I was "murdered" for doing so[167].

4.4.2 Evidence Science and the Discovery of New Evidence

I understand that the discovery of new evidence depends on the nature of the investigations that take place in the substantive area of concern. The evidence we generate or discover in any context depends upon the questions we ask. People in different contexts will naturally ask different questions. Thus, a historian, a sociologist, an accident investigator, and a physician will ask different questions and will generate the different kinds of evidence of interest to them. The path to expertise in any area depends in no small part on knowing what kinds of questions to ask and how answers to them might be obtained. It is also true that persons having different standpoints will ask different questions in the same context. Suppose a police officer, a news reporter, and an attorney all arrive at the scene involving an injured or a dead person. The police officer will ask whether a crime has been committed. The reporter wil ask whether there is a story here. And the attorney will ask whether there is a  civil complaint or a criminal charge that can be levied in a legal action of some sort.

But it is also true in so many situations involving discovery or investigative efforts that we have hypotheses in search of evidence at the same time we have potential evidence in search of hypotheses. It turns out that we can generate new evidence in both of these situations. I have already noted that from hypotheses we generate new evidence and new lines of reasoning. But new evidence can be generated by several other ways as I now illustrate.